最適化勉強会 ~数理最適化を使用してシフトスケジューリング問題を解く~
こんにちは。NRIデジタルの難波です。
NRIデジタルのAIビジネスイノベーションチームでは、定期的に最適化勉強会を開催しています。
今回は最適化勉強会にて取り扱ったシフトスケジューリング問題について、具体例を用いて紹介します。細かな問題設定やシフト表の出力は、ほとんどの人が一度は使ったことのあるExcelで行います。
また、シフト表の作成には汎用性の高さで人気のプログラミング言語Pythonを使用します。
シフトスケジューリング問題とは
昨今、働き方改革の浸透により、人々の働き方は多岐にわたります。働き方の一つに、従業員が時間交代制で働くシフト制の勤務形態があります。
シフトスケジューリング問題とは、「どの従業員が・いつ・どのシフトに入るか」を決定する問題のことです。手作業でシフトを決定しようとすると、「夜のシフトはx人必要で、、、」「○○さんと△△さんは水曜日しか出られなくて、、、」「学生の□□さんは所得がxxx万円を超えそうだから調節しないと、、、」など、考慮しなければならないことが多くあり、かなりの時間がかかってしまいます。
そこで、数理最適化を使用することで、シフトスケジューリング問題を自動で解くことができるようになります。
数理最適化による問題設定
数理最適化では、シフトスケジューリング問題を解く際、「どの従業員が・いつ・どのシフトに入るか」を「決定変数」として定義し、考慮しなければならない条件を「制約」として数式で表現します。そして、制約を満たしながら、どんなスケジュールを作成したいかを「目的関数」として定義します。目的関数を最大化または最小化することで、スケジュールを作成することができます。
決定変数はxijt(従業員iがシフトjに日tに勤務する場合1、そうでない場合は0となる変数)として定義することで、「どの従業員が・いつ・どのシフトに入るか」を表現することができます。
考慮しなければならない条件(以下制約)は、必ず守らなければならないハード制約と、なるべく守るべきソフト制約に分類されます。ハード制約は、「4週に4回休日がなければならない」などの労働基準法による制約や、「この時間帯のシフトには何人以上必要」などの施設特有の制約などが含まれます。ソフト制約は、「Aさんは夜勤になるべく入りたくない」「Bさんは今月たくさん稼ぎたい」などの従業員の希望による制約が例として挙げることができます。
それでは、あるスーパーマーケットのアルバイトのシフトを例として、シフトスケジューリング問題を解いていきます。
スーパーマーケットのシフトスケジューリング問題
あるスーパーマーケットについて、早番、日勤、夜勤の3つのシフトに、パートタイム職員(アルバイト)を30人当てはめることを考えます。条件は以下の通りです。
| シフト | 早番 | 日勤 | 遅番 |
|---|---|---|---|
| 必要シフト人数 | 4 | 8 | 3 |
| 給与(円) | 15000 | 10000 | 10000 |
| 従業員No | 特徴 |
|---|---|
| 1-10 | 特徴がなく、あまりシフトに対して文句を言わない |
| 11-20 | ハードワークでもいいので、たくさん稼ぎたい |
| 21-30 | なるべく遅番に入りたくない |
| ハード制約 (必ず守る) |
週に7日以上働いてはいけない |
| 10連勤以上は禁止とする | |
| 遅番は連続二回までしか許されない | |
| 遅番の次のシフトは遅番でなくてはいけない | |
| ソフト制約 (出来れば守る) |
No.11-20は月の合計給与をなるべく大きくする |
| No.21-30はなるべく遅番に入らないようにする |
しかし、合計給与と遅番割当数では単位が異なるため、重みの設定には注意が必要です。例えば、w1=w2=1 と設定すると、目的関数に対して、合計給与と比べて遅番割当数の影響がかなり小さくなってしまいます。これに対し、w1=1,w2=20000などに設定することで、「従業員No.21-30に1回遅番を割り当てることは、従業員No.11-20の合計給与を20000円減少させる」と解釈することができます。
このように、シフト作成者は従業員No.21-30に遅番を割り当てることの経済的リスクを加味して、重みを設定する必要があります。
結果出力
先に述べた問題設定でシフトスケジューリング問題を解いていきます。
今回は前述した従業員数やシフト数等の問題設定で行いますが、下記画像のようにExcelで設定することができます。
シフト表作成の仕組みは以下の通りです。
まず、「勤務表作成」ボタンが押されることによってマクロが起動し、Pythonスクリプトが実行されます。Pythonスクリプトでは、Excelで設定された値を読み込み、数理最適化のモデルを記述するためのライブラリであるPuLPを使用して問題の記述および求解しています。そして、導き出されたスケジュールはxlwingsというライブラリを使用してExcelにシフト表として出力しています。
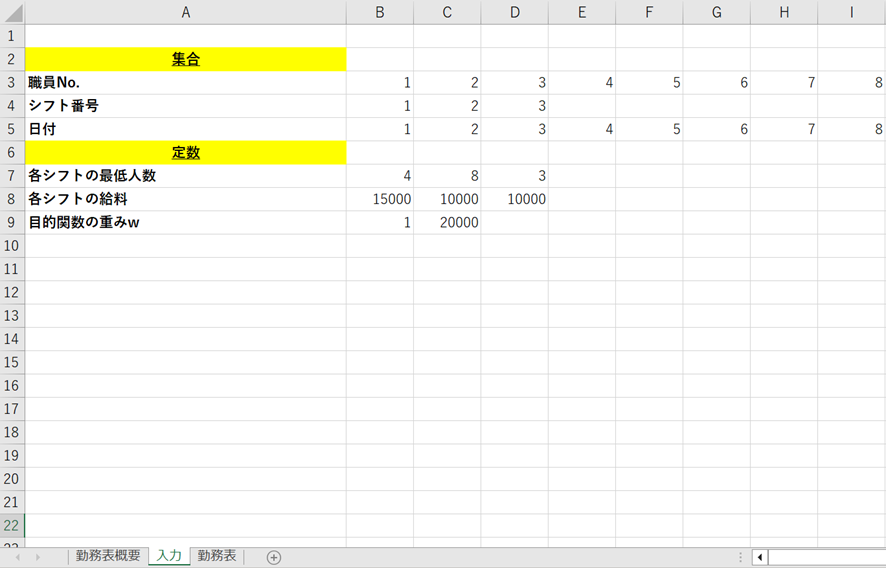
シフト作成者は入力用のExcelシートを埋めて、「勤務表作成ボタン」を押すことでシフト表を作成することができます。
重みをw1=1,w2=20000として設定し、作成されたシフト表は下記の図の通りです。

このシフト表から、たくさん稼ぎたい従業員No.11-20は、他の従業員よりも多くのシフトに割り当てられていることがわかります。また、遅番に入りたくない従業員No.21-30は、遅番に一度も割り当てられていないことが確認できます。
これは、目的関数における従業員No.11-20の合計給与を増加させ、従業員No.21-30の遅番割当数を減少させる影響が反映されているためです。しかし、その代わりに従業員No.1-10は、シフトにあまり入れておらず、多くの遅番に割り当てられていることがわかります。
また、たくさん稼ぎたい従業員No.11-20にも必ず何日か休みが割り当てられています。これは、制約として設定した「週に7日以上働いてはいけない」や「10連勤以上は禁止とする」が正しく機能しているためです。このように、シフト表に目的関数と制約の影響が適切に反映していることが確認できます。なお、シフト表の作成に要する実行時間は10秒未満であり、効率的にシフト表が作成されていることがわかります。
数理最適化を用いてシフトスケジューリング問題を解くことによって、制約および従業員の希望を満たすスケジュールを作成することができました。しかし、複雑な制約が追加されたり、従業員数やシフト数が増加したりすると、実行時間が長くなってしまうことは留意しなくてはなりません。
おわりに
今回は、数理最適化を用いたシフトスケジューリング問題の解法を、具体例を用いて紹介しました。本記事を通じて、数理最適化を含む最適化問題について少しでも興味をもっていただけるとうれしいです。
NRIデジタルでは、配送最適化をはじめとするさまざまな最適化問題に取り組んでいます。実際の最適化問題は、今回取り扱ったような簡単な設定ではなく、複雑な問題設定になることが多いため、求解の難易度が大きく異なります。「これを最適化したいけど、方法がわからない、、、」「簡単な問題は最適化できるけど、複雑になると解けなくなる、、、」といったお悩みをお持ちのお客さまは、ぜひNRIデジタルにご相談ください。
