最適化勉強会　～深層強化学習による在庫最適化～

泉裕紀

2024.8.6

こんにちは。NRIデジタルの泉です。
NRIデジタルでは、社内で最適化問題を業務で扱っているメンバーを中心に、知識向上のために「最適化勉強会」が開催されています。本記事は社内の最適化勉強会にて発表した「深層強化学習による在庫最適化」についての記事になります。

強化学習とはなにか

強化学習とは、機械学習の一種です。INPUT情報として「状態（今どうなっているか）」を受取り、「報酬」が多いもしくは「罰則」が少ないと思われる「行動」を決定します。実際の「報酬」や「罰則」を元にその行動を取るのが正しかったのかを振り返ります。これを繰り返し行い、「状態」に対してより良い「行動」を選べるようになっていくことを目指します。

強化学習の限界と深層強化学習

強化学習では、「状態」に対して「報酬」が多くなる or 「罰則」が少なくなるような「行動」を取りたいです。これを表形式でデータを保持しています。その表では、行が「状態」、列が「行動」、値が「報酬」を表しています。例えば、以下の表を保持していたとすると、現在の状態が1のときは左に行くと報酬が0で右に行くと報酬が1になるので、右に行くべきということがわかります。

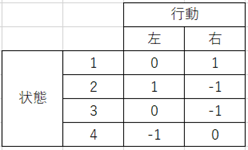
上記のように状態のパターンの数・行動のパターンの数が少なければ表形式で十分表現することができますが、現実の問題を考えると状態のパターンや行動のパターンが非常に大きくなってしまい、表形式で表すのにも限界があります。

そこで、この状態と行動による想定報酬の決定をニューラルネットワークで表現しようとしたのが、深層強化学習になります。深層強化学習の主な活用事例には、囲碁AIの「AlphaGo」があります。プロ棋士に勝利をしたことで大きな話題になりました。その他にもロボットの制御や自動運転などの技術に用いられることがあります。

今回は、この深層強化学習を使って商品の在庫数の最適化をすることを考えます。

今回の問題設定について

3つの商品A, B, Cの在庫数を、売り切れにならないように気をつけつつ在庫数はなるべく少なめに管理したいという問題を考えます。倉庫のスペースは十分大きく、他の商品との兼ね合いなどは考慮の必要が無いものとし、各商品は発売してから十分な日付が経っており、以下のように売上傾向が予測できるものとします。

商品A
販売個数の平均 : 300、　標準偏差 : 50
各曜日の売上率(倍) : [月, 火, 水, 木, 金, 土, 日] = [1.1, 1.1, 1.1, 1.1, 1.1, 0.75, 0.75]
各月の売上率(倍) : [1月, 2月, …, 12月] = [0.7, 0.5, 0.7, 1, 1, 1, 1.3, 1.5, 1.3, 1, 1, 1]
発注1ロットあたりの商品数 : 10個
商品B
販売個数の平均 : 1000、　標準偏差 : 100
各曜日の売上率(倍) : [月, 火, 水, 木, 金, 土, 日] = [0.8, 0.8, 0.8, 0.8, 0.8, 1.5, 1.5]
各月の売上率(倍) : [1月, 2月, …, 12月] = [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
発注1ロットあたりの商品数 : 30個
商品C
販売個数の平均 : 1200、　標準偏差 : 200
各曜日の売上率(倍) : [月, 火, 水, 木, 金, 土, 日] = [0.8, 0.8, 0.8, 0.8, 0.8, 1.5, 1.5]
各月の売上率(倍) : [1月, 2月, …, 12月] = [1.3, 1.5, 1.3, 1, 1, 1, 0.7, 0.5, 0.7, 1, 1, 1]
発注1ロットあたりの商品数 : 50個

また、キャンペーンの発生タイミングは各商品ランダムなタイミングで事前に決定しているものとします。その期間は7日間で、その間の販売個数が1.5倍になるとします。発注から次回発注までの間隔は1日（毎日発注可能）で、発注から入荷までのリードタイムは3日とします。
これを元に1年間の在庫数最適化を行いました。

深層強化学習について

深層強化学習のモデルとしては、行動（今回では、商品を何ロット入荷するのか）の値が連続値であることを許すアルゴリズムとして、今回はDeep Deterministic Policy Gradient ( DDPG ) を採用しました。

深層強化学習と比較するための在庫数決定ルールについて

とします。一般的に用いられる安全在庫理論に基づいて、上記を設定しました。
発注点を下回ったとき、適正在庫数以下を満たすなるべく大きな発注ロット数だけ発注することにします。

検証時の各商品の販売個数の推移

各商品の販売個数の推移は以下のようになりました。

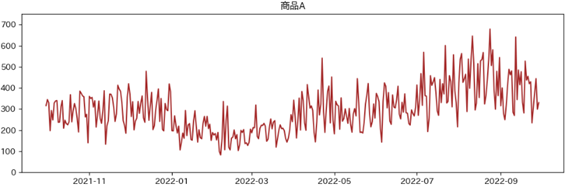
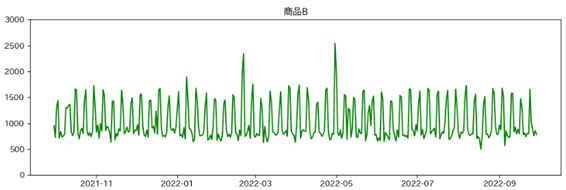
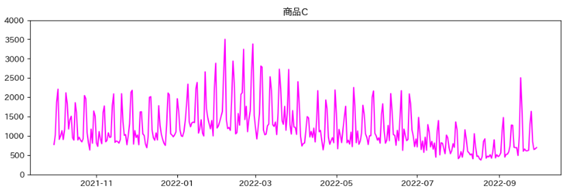
深層強化学習とルールベースの比較

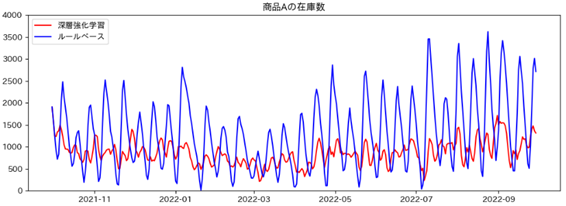
各商品の在庫数の推移は以下のようになりました。
全体的に深層強化学習の方がルールベースに比べて在庫数少なく安定しており、在庫切れした回数も少ないという結果になりました。

商品数Aの在庫数
深層強化学習　平均 : 867.6個　標準偏差 : 272.7　在庫切れした回数 : 0回
ルールベース　平均 : 1298.7個　標準偏差 : 790.2　在庫切れした回数 : 0回

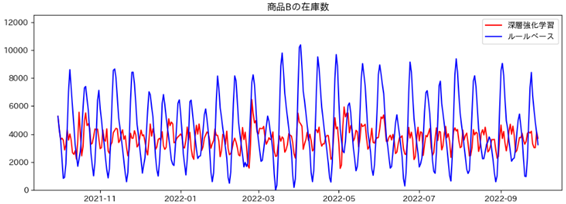
商品数Bの在庫数
深層強化学習　平均 : 3687.3個　標準偏差 : 755.6　在庫切れした回数 : 0回
ルールベース　平均 : 4293.5個　標準偏差 : 2369.6　在庫切れした回数 : 1回

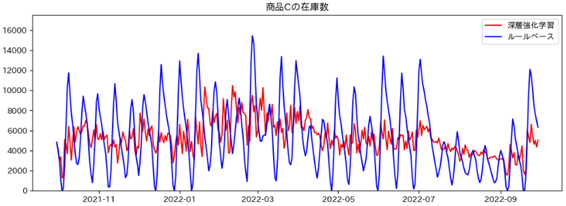
商品数Cの在庫数
深層強化学習　平均 : 5296.3個　標準偏差 : 1607.8　在庫切れした回数 : 0回
ルールベース　平均 : 5323.7個　標準偏差 : 3353.9　在庫切れした回数 : 9回

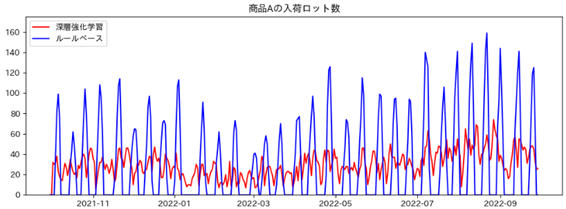
また、各商品の入荷ロット数は下記のようになりました。
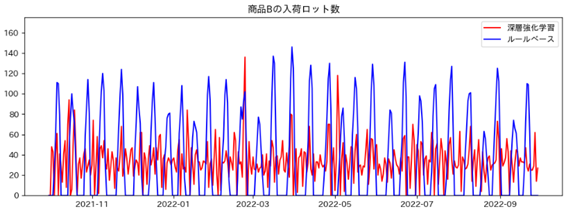
全体的に深層強化学習の方がルールベースに比べて、入荷ロット数が安定していることがわかります。

商品Aの入荷ロット数
深層強化学習　平均 : 29.7個　標準偏差 : 12.8個
ルールベース　平均 : 30.0個　標準偏差 : 40.2個

商品Bの入荷ロット数
深層強化学習　平均 : 33.8個　標準偏差 : 19.0個
ルールベース　平均 : 33.7個　標準偏差 : 41.8個

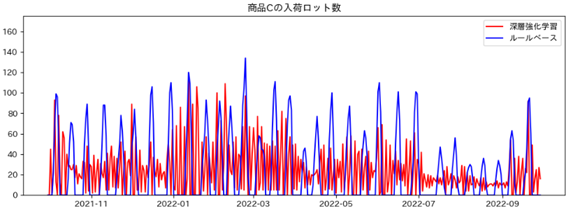
商品Cの入荷ロット数
深層強化学習　平均 : 24.2個　標準偏差 : 23.2個
ルールベース　平均 : 24.0個　標準偏差 : 33.3個

おわりに

以上の結果から、ルールベースに比べて深層強化学習の方が在庫数を少なくするだけではなく、安定して管理することができることがわかりました。
「在庫数をなるべく少なくする」という方針で学習していましたが、在庫数を少なくした結果、ルールベースよりも安定的に入荷することになったのだと思われます。
このようにNRIデジタルでは、日々の業務だけでなく、技術力の研鑽も継続的に行っています。