最適化勉強会 ~最大マッチング問題とその応用 前編~
こんにちは。NRIデジタルの泉です。
NRIデジタルでは、業務にてデータサイエンスとして機械学習だけでなく最適化問題を取り扱うことがあります。最適化問題には、解決したい課題に対して最適な解答を得ることができるという特徴があるからです。とはいえ、現実の問題をすべて最適化問題で解けるわけではありません。最適化問題で解くためには、現実の問題を数式で表現する必要がありますし、大量のデータで最適化問題を解こうとすると非常に時間がかかってしまって現実的では無いことがよくあります。こういったケースには機械学習が役立ちます。
こういった背景があり、社内で最適化問題を業務で扱っているメンバーを中心に、知識向上のために「最適化勉強会」が開催されています。
さて、本記事では社内の最適化勉強会にて発表した「最大マッチング問題とその応用」について、数学的な回りくどい説明をできる限り省いて実際にありえそうな問題とその解き方を2回に分けてご紹介していきたいと思います。
問題① 二部グラフにおける最大マッチング問題
以下のような3対3の合コンを考えてみます。男女間には、お互いがペアになっても良いと思っている場合に辺が結ばれています。
ここですべての人は、複数の異性とペアになることはできないとします。
このとき、男女ペア(以降、マッチングと呼びます)の最大化を行う問題が最大マッチング問題です。
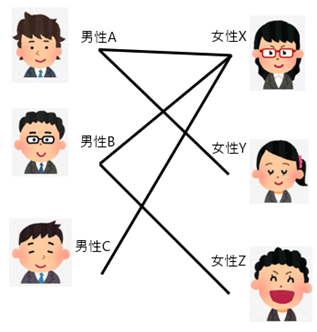 最大マッチング問題の例:3対3合コン
最大マッチング問題の例:3対3合コン後の説明のために、男性Aと女性Xがマッチングであるとき、男性Aと女性Xを結ぶ辺をマッチングの辺とよび、マッチングでないときにはマッチングでない辺と呼ぶことにします。また、男性Aと女性Xを結ぶ辺を(男性A, 女性X)で表すことにします。
最大マッチング問題を解く上で重要になる考え方が「増加道」です。
実は「増加道」があれば、現状見つかっているマッチングよりも大きなマッチングを見つけることができ、「増加道」がなければ、現状見つかっているマッチングが最大マッチングになります。
増加道とは、以下のようなマッチングが見つかっていない人から始まり、最終的にマッチングが見つかっていない人までつながる辺の集合であり、その間に経由した人は必ずマッチングが見つかっている人という特徴を持ちます。
 増加道
増加道つまり、上図のようなマッチングでない辺、マッチングの辺、マッチングでない辺…と繰り返し、最後がマッチングでない辺になっているものが増加道です。
この時、増加道はマッチングの辺の数 + 1 = マッチングでない辺の数が成立します。
この増加道に対して、マッチングの辺をマッチングでない辺に、マッチングでない辺をマッチングの辺に置き換えることで、より大きなマッチングを見つけることができることがわかっています。1)Two Theorems in Graph Theory | Claude Berge
実際に上記の例を解いてみようと思います。
最初にマッチングはまだ見つかってないものとします。
ここで増加道を探します。{ (男性A, 女性X) } が増加道です。マッチングでない辺しかないため、これをマッチングの辺にすると、{ (男性A, 女性X) }がマッチングになります。
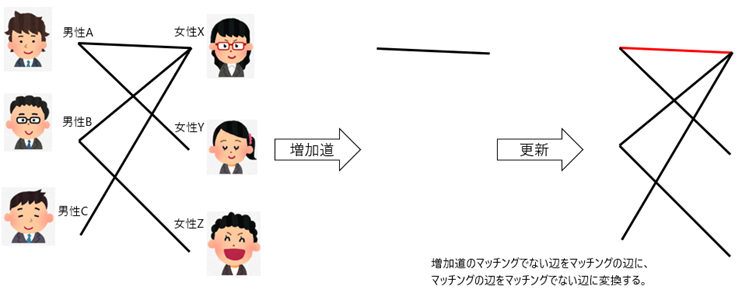 一回目の更新
一回目の更新さらに増加道を探すと、{ (男性B, 女性X), (女性X, 男性A), (男性A, 女性Y) }が見つかります。マッチングの辺をマッチングでない辺に、マッチングでない辺をマッチングの辺に置き換えると{ (男性A, 女性Y), (男性B, 女性X) }がマッチングになります。
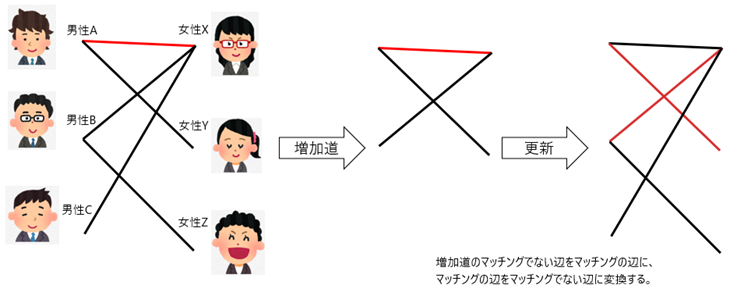 二回目の更新
二回目の更新さらに増加道を探すと、{ (男性C, 女性X), (女性X, 男性B), (男性B, 女性Z) }が見つかります。マッチングの辺をマッチングでない辺に、マッチングでない辺をマッチングの辺に置き換えると{ (男性A, 女性Y), (男性B, 女性Z), (男性C, 女性X) }がマッチングです。
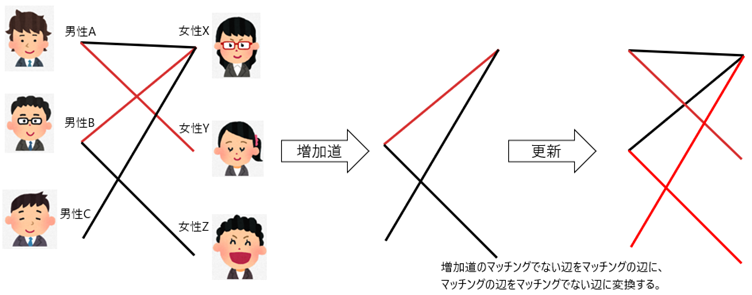 三回目の更新
三回目の更新これで、マッチングがみつかっていない人が存在しないため増加道が存在しないので、{ (男性A, 女性Y), (男性B, 女性Z), (男性C, 女性X) }が最大マッチングとなります。
全員が納得できる男女ペアを見つけることができました。
問題②:二部グラフにおける最大1対多マッチング問題
以下のような保育園への子供の割当問題を考えてみます。
保育園と子供の間には、通える距離であれば辺が結ばれています。
保育園には予め預けることができる子供の人数が決まっており(保育園Aは2人、保育園Bは3人)、その数以下の子供とマッチングすることができるとします。また、子供が通うことのできる保育園は1つに限るものとします。このとき保育園に通うことのできる子供の数の最大化を行う問題が最大1対多マッチング問題です。
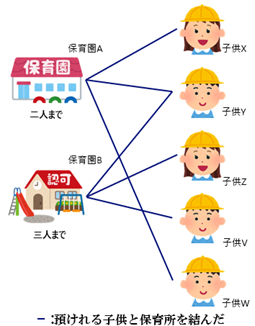 最大1対多マッチング問題の例:保育園への子供の割当
最大1対多マッチング問題の例:保育園への子供の割当保育園A、保育園Bをそれぞれ預けることができる子供の数である2つ, 3つに分割を行い、元々の保育園と同じ子供に辺を結ぶことでこの問題は最大マッチング問題に帰着することができます。分割した結果は下図になります。
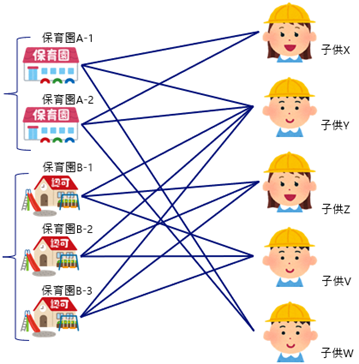
実際に上記の例を解いてみようと思います。
最初にマッチングはまだ見つかってないものとします。
ここで増加道を探します。{ (保育園A-1, 子供X) } が増加道です。マッチングでない辺しかないため、これをマッチングの辺にすると、{ (保育園A-1, 子供X) }がマッチングになります。
さらに増加道を探すと、{ (保育園A-2, 子供X), (子供X, 保育園A-1), (保育園A-1, 子供Y) }が見つかります。マッチングの辺をマッチングでない辺に、マッチングでない辺をマッチングの辺に置き換えると{ (保育園A-1, 子供Y), (保育園A-2, 子供X) }がマッチングになります。
これを繰り返していくと最終的には下図のようにマッチング{ (保育園A-1, 子供X), (保育園A-2, 子供W), (保育園B-1, 子供V), (保育園B-2, 子供Z), (保育園B-3, 子供Y) }を見つけることができます。
これでマッチングできていない子供がいないため、これが最大マッチングとなります。
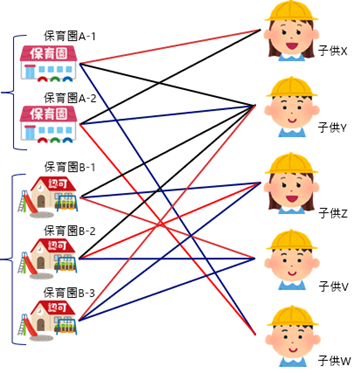
この結果を元に、分割した頂点を元に戻します。辺を統合する際にマッチングの辺が存在していればマッチングの辺とします。この結果得られたものが下図になります。
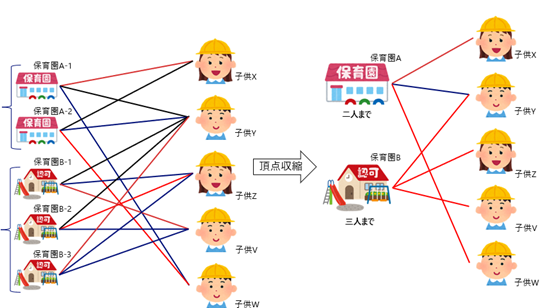
この結果、得られたマッチング{ (保育園A 子供X), (保育園A, 子供W), (保育園B, 子供V), (保育園B, 子供Z), (保育園B, 子供Y) }が最大1対多マッチングになります。
今回のケースではすべての保育園が上限まで子供を割り当てされましたが、全体最適のために上限を下回る子供を割り当てることが必要になることもあります。
おわりに
今回は社内の最適化勉強会にて発表した「最大マッチング問題とその応用」について紹介させていただきました。後編ではさらなる応用問題について考えていきます。
この記事を読んで、最適化問題の魅力を少しでも伝えることができたら幸いです。
References
